KMP算法

Posted on | In | |

KMP概述

KMP算法是由D.E.Knuth、J.H.Morris和V.R.Pratt三个人共同提出的，就取三个人名字的首字母作为该算法的名字。KMP主要解决的是目标字符串（target）中的模式（pattern）定位问题，例如：

有一个模式串P，如果它在一个主串T中出现，则返回它第一次出现的起始位置，否则返回-1。

KMP算法与暴力解法的区别就在于KMP算法巧妙的消除了指针i（主串中的指针）的回溯问题，只需确定下次匹配j（模式串中的指针）的位置即可，使得问题的复杂度由O(m * n)下降到O(m + n)。

从暴力解法入手：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int pattern_match(string T, string P) {
    int i = 0, j = 0;
    while (i < T.length() && j < P.length()) {
        if (T[i] == P[i]) {
            i++;
            j++
        } else {
            i = i - j + 1;
            j = 0;
        }
    }

    return j == P.length ? i - j : -1;
}

再考虑下面这种情况：

kmp1

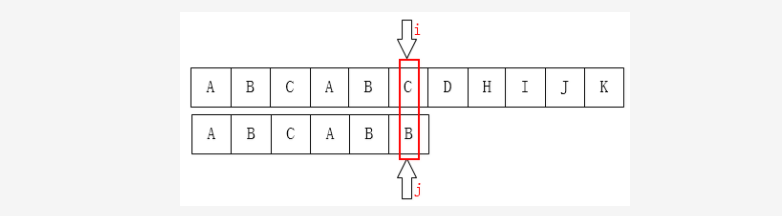
此时发生了字符串的不匹配后，按照暴力解法，还需要将i设置为1，j设置为0，显然是不合理的，因为在遍历过程中，我们已经“知道”T中有“ABC”串，而P也是由“ABC”串开头，理想情况下下一步的移动应该是这样：

kmp2

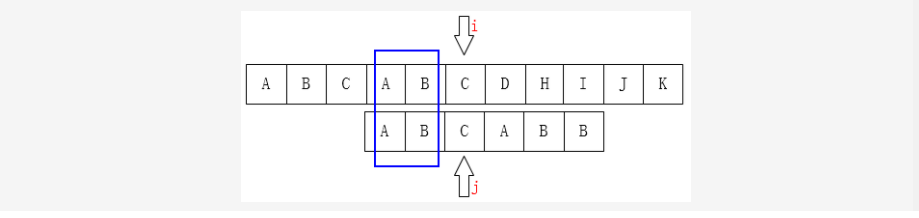
而这，也正是KMP想解决的问题。这样，可以有效的避免了i的回溯，即i不会向前移动了，只需要移动j的位置即可。

KMP的核心在于next数组，其中，next[k]表示：当T[i] != P[j]时，指针j应该移动到的位置。即每当产生不匹配时，利用next[j]来决定j的下一个位置。

首先我们假设已经通过计算得到了完整的next数组，利用它完成匹配的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int KMP_match(string target, string pattern) {
    if (pattern == "")
        return 0;
    vector<int> next = getNext(pattern);
    for (int i = 0, j = 0; i < target.length(); ) {
        if (j == -1 || target[i] == pattern[j]) {
            if (j == pattern.length() - 1)
                return i - j;
            i++;
            j++;
        }
        else {
            j = next[j];
        }
    }
    return -1;
}

接下来，如何得到next？

利用部分匹配值求解

next的求解方法有几种，其中根据KMP原作者的思路，利用”Partial Match Table“（部分匹配表）的方法，可以参考字符串匹配的KMP算法——阮一峰中的详细图解。其重点在于计算模式串P的前缀和后缀的部分匹配值（Partial Match Value）。计算该表的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
vector<int> partialMatching(string pattern) {
    vector<int> pMatch(pattern.length(), 0);
    int k = 0;
    for (int i = 1; i < pattern.length(); i++) {
        while (k > 0 && pattern[k] != pattern[i])
            k = pMatch[k - 1];
        if (pattern[k] == pattern[i])
            k = k + 1;
        pMatch[i] = k;
    }
    return pMatch;
}

整个P串的部分匹配值组成了完整的部分匹配表，利用该表即可完成P不匹配后的移位：

移动位数 = 已匹配的字符数 - 对应的部分匹配值

即，利用该表可得到next：

1
next[j] = j - pMatch[j - 1];

递推法求解

同时，也可以使用递推法得到整个next数组。

首先，根据定义，next[0] = -1。假设next[j] = k, 即P[0...k-1] == P[j-k, j-1]：

  • 若P[j] == P[k]，则有P[0..k] == P[j-k,j]，很显然，next[j+1] = next[j] + 1;
  • 若P[j] != P[k]，则可以把其看做模式匹配的问题（即整个KMP算法要解决的问题），即匹配失败的时候，k值如何移动，显然k = next[k]。

由以上思路，不难得到递推法的求解next的代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
vector<int> getNext(string pattern) {
    vector<int> next(pattern.length(), 0);
    next[0] = -1;
    for (int j = 0, k = -1; j < pattern.length() - 1; ) {
        if (k == -1 || pattern[j] == pattern[k]) {
            next[j + 1] = k + 1;
            j++;
            k++;
        }
        else {
            k = next[k];
        }
    }
    return next;
}

如果难以理解递推法的推导过程，可以参考详解KMP算法。

本文为博主原创文章，转载请注明出处。